Resources for the second edition are here. I'd love to know what you think about Python Crash Course; please consider taking a brief survey. If you'd like to know when additional resources are available, you can sign up for email notifications here.

Solutions - Chapter 15

Back to solutions.

15-1: Cubes

A number raised to the third power is a cube. Plot the first five cubic numbers, and then plot the first 5000 cubic numbers.

Plotting 5 cubes:

from matplotlib import pyplot as plt

# Define data.
x_values = [1, 2, 3, 4, 5]
cubes = [1, 8, 27, 64, 125]

# Make plot.
plt.scatter(x_values, cubes, edgecolor='none', s=40)

# Customize plot.
plt.title("Cubes", fontsize=24)
plt.xlabel('Value', fontsize=14)
plt.ylabel('Cube of Value', fontsize=14)
plt.tick_params(axis='both', labelsize=14)

# Show plot.
plt.show()

Output:

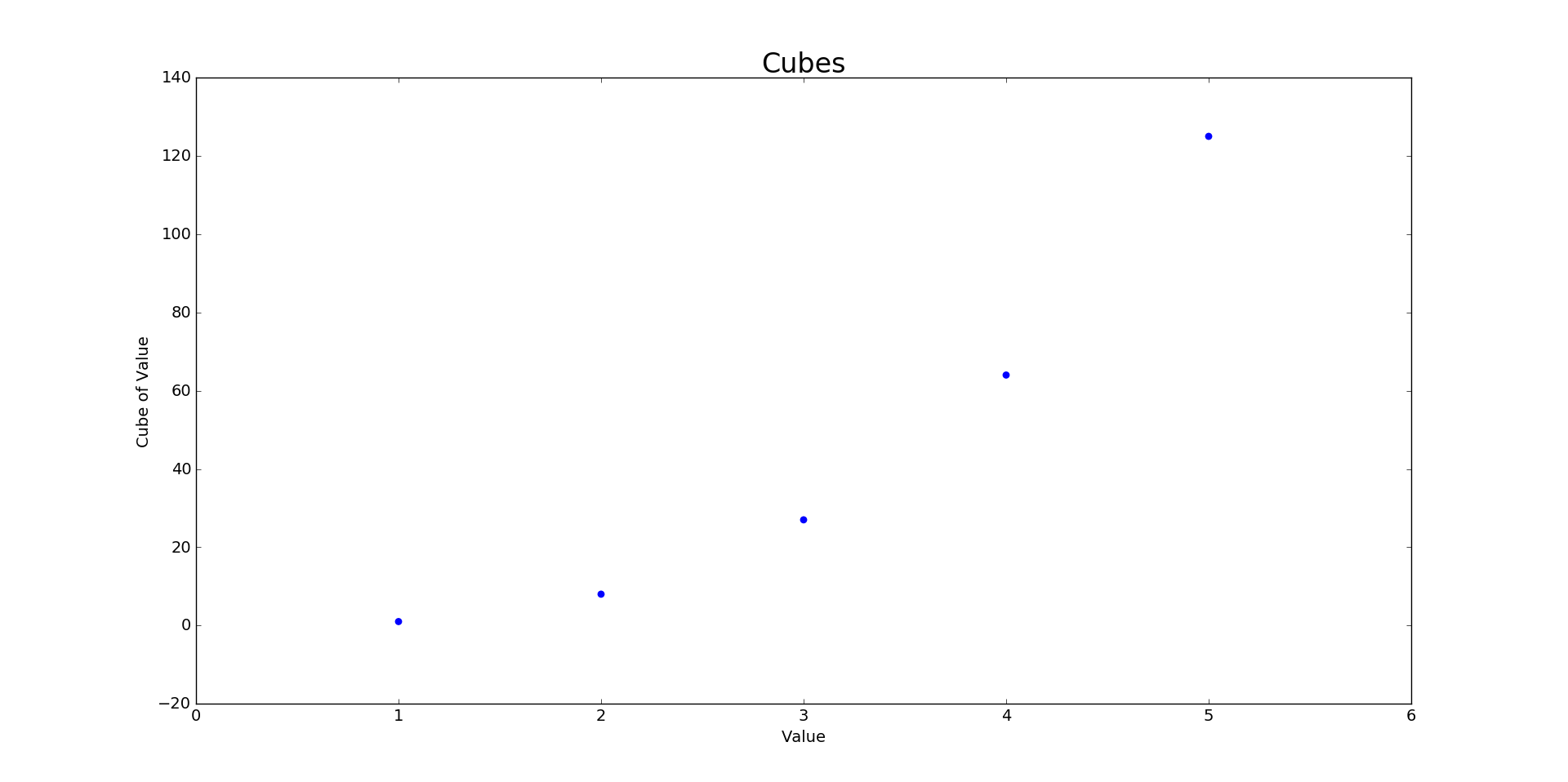
Plot showing 5 cubes

Plotting 5000 cubes:

from matplotlib import pyplot as plt

# Define data.
x_values = list(range(5001))
cubes = [x**3 for x in x_values]

# Make plot.
plt.scatter(x_values, cubes, edgecolor='none', s=40)

# Customize plot.
plt.title("Cubes", fontsize=24)
plt.xlabel('Value', fontsize=14)
plt.ylabel('Cube of Value', fontsize=14)
plt.tick_params(axis='both', labelsize=14)
plt.axis([0, 5100, 0, 5100**3])

# Show plot.
plt.show()

Output:

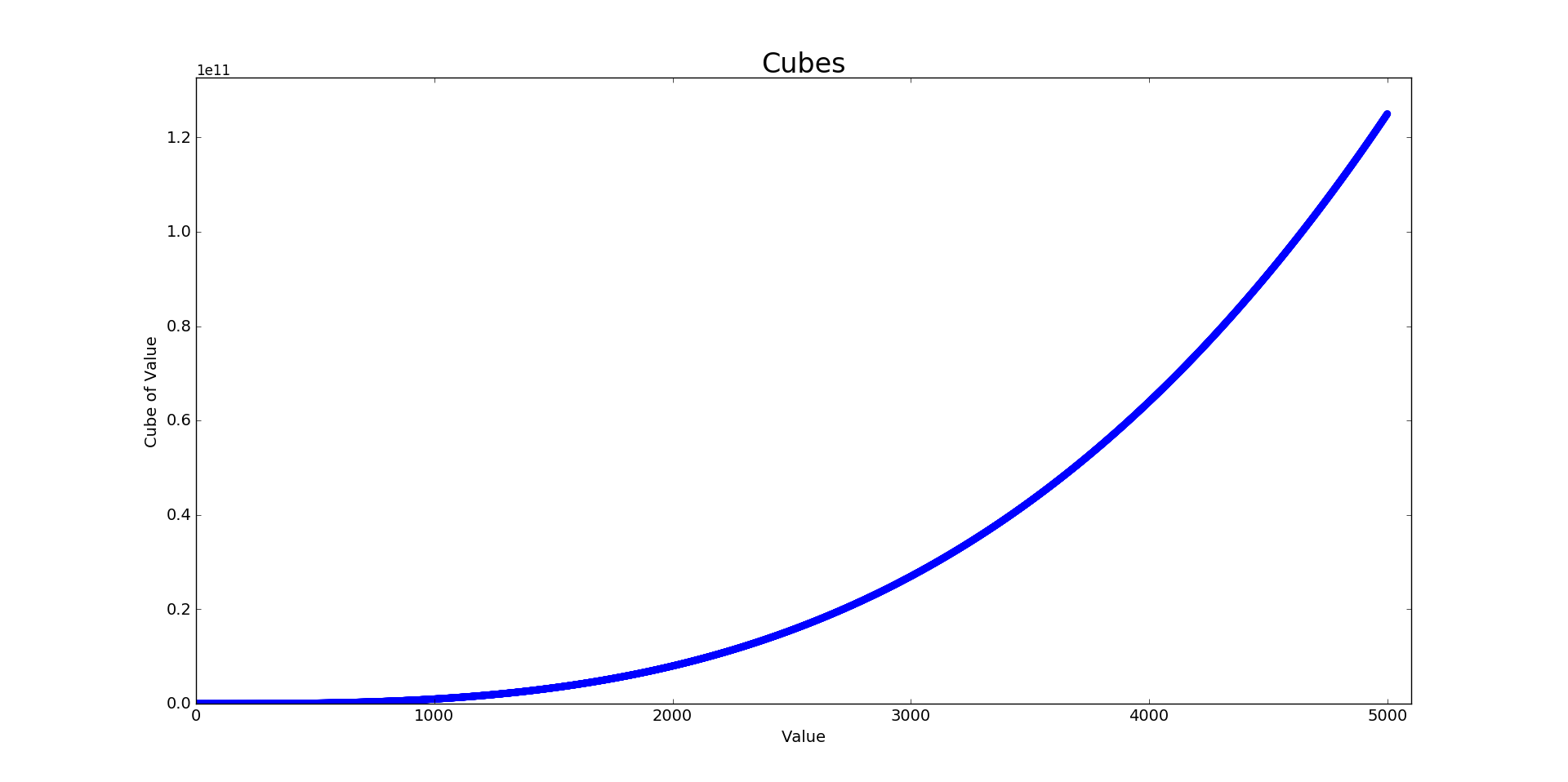
Plot showing 5000 cubes

top

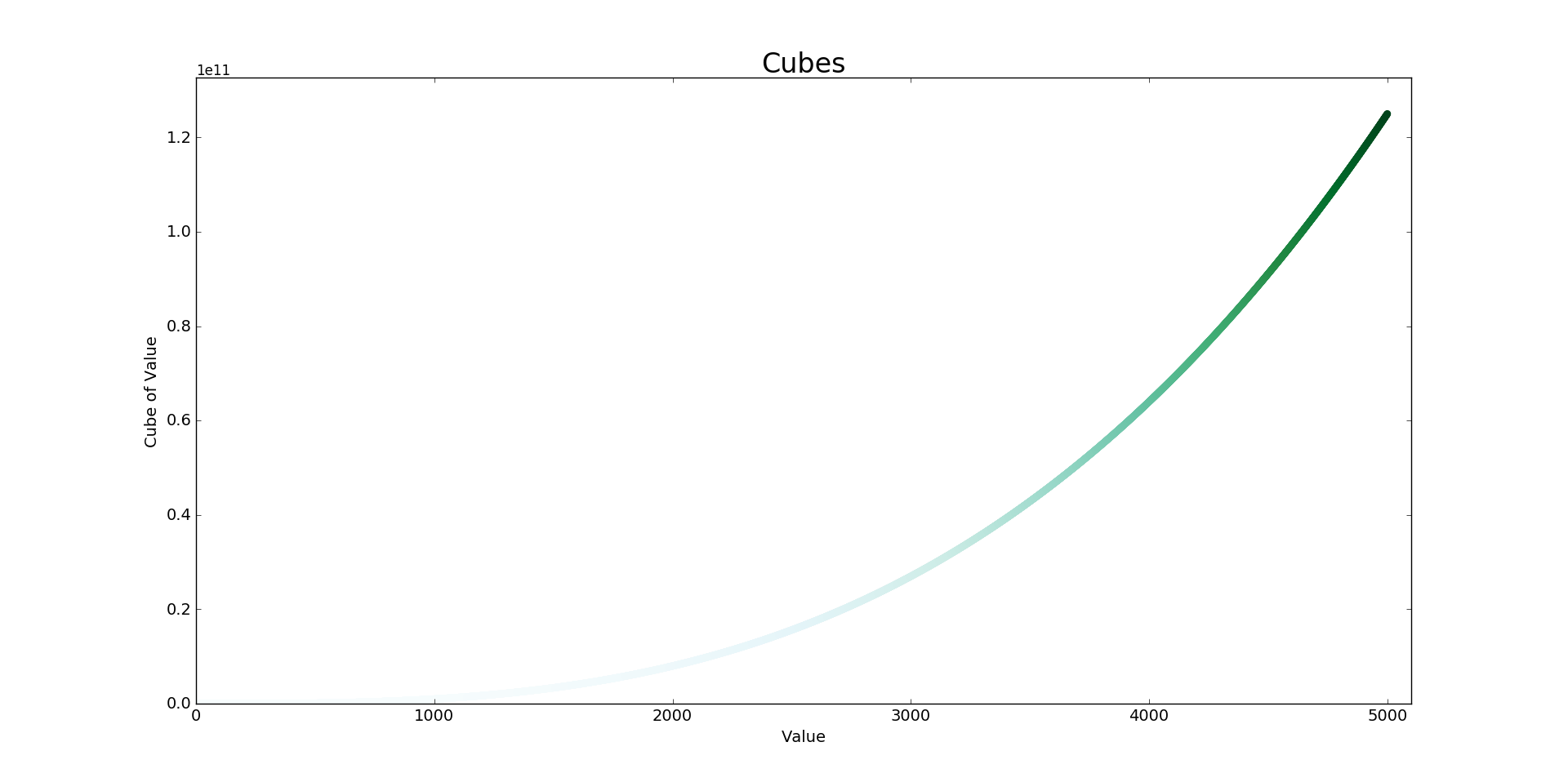
15-2: Colored Cubes

Apply a colormap to your cubes plot.

from matplotlib import pyplot as plt

# Define data.
x_values = list(range(5001))
cubes = [x**3 for x in x_values]

# Make plot.
plt.scatter(x_values, cubes, edgecolor='none', c=cubes, cmap=plt.cm.BuGn, s=40)

# Customize plot.
plt.title("Cubes", fontsize=24)
plt.xlabel('Value', fontsize=14)
plt.ylabel('Cube of Value', fontsize=14)
plt.tick_params(axis='both', labelsize=14)
plt.axis([0, 5100, 0, 5100**3])

# Show plot.
plt.show()

Output:

Plot showing 5000 cubes, using a colormap

top

15-3: Molecular Motion

Modify rw_visual.py by replacing plt.scatter() with plt.plot(). to simulate the path of a pollen grain on the surface of a drop of water, pass in the rw.x_values and rw.y_values, and include a linewidth argument. Use 5000 instead of 50,000 points.

import matplotlib.pyplot as plt

from random_walk import RandomWalk

# Keep making new walks, as long as the program is active.
while True:
    # Make a random walk, and plot the points.
    rw = RandomWalk(5000)
    rw.fill_walk()
    
    # Set the size of the plotting window.
    plt.figure(dpi=128, figsize=(10, 6))
    
    point_numbers = list(range(rw.num_points))
    plt.plot(rw.x_values, rw.y_values, linewidth=1)
        
    # Emphasize the first and last points.
    plt.scatter(0, 0, c='green', edgecolors='none', s=75)
    plt.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolors='none',
        s=75)
        
    # Remove the axes.
    plt.axes().get_xaxis().set_visible(False)
    plt.axes().get_yaxis().set_visible(False)
        
    plt.show()
    
    keep_running = input("Make another walk? (y/n): ")
    if keep_running == 'n':
        break

Output:

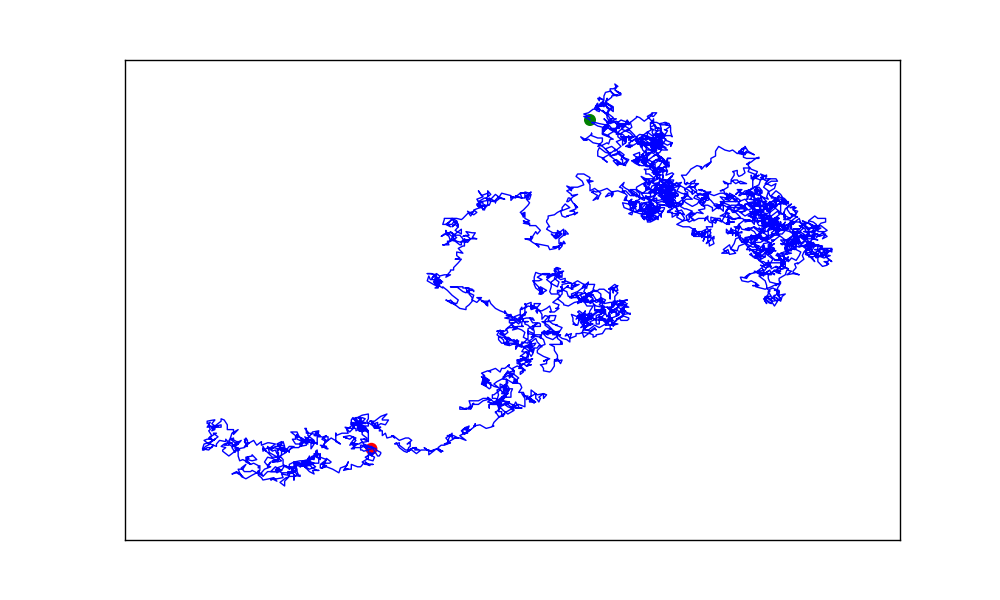
Random walk with 5000 points, connected by lines

The scatter plots appear behind the lines. To place them on top of the lines, we can use the zorder argument. Plot elements with higher zorder values are placed on top of elements with lower zorder values.

import matplotlib.pyplot as plt

from random_walk import RandomWalk

# Keep making new walks, as long as the program is active.
while True:
    # Make a random walk, and plot the points.
    rw = RandomWalk(5000)
    rw.fill_walk()
    
    # Set the size of the plotting window.
    plt.figure(dpi=128, figsize=(10, 6))
    
    point_numbers = list(range(rw.num_points))
    plt.plot(rw.x_values, rw.y_values, linewidth=1, zorder=1)
        
    # Emphasize the first and last points.
    plt.scatter(0, 0, c='green', edgecolors='none', s=75, zorder=2)
    plt.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolors='none',
        s=75, zorder=2)
        
    # Remove the axes.
    plt.axes().get_xaxis().set_visible(False)
    plt.axes().get_yaxis().set_visible(False)
        
    plt.show()
    
    keep_running = input("Make another walk? (y/n): ")
    if keep_running == 'n':
        break

Output:

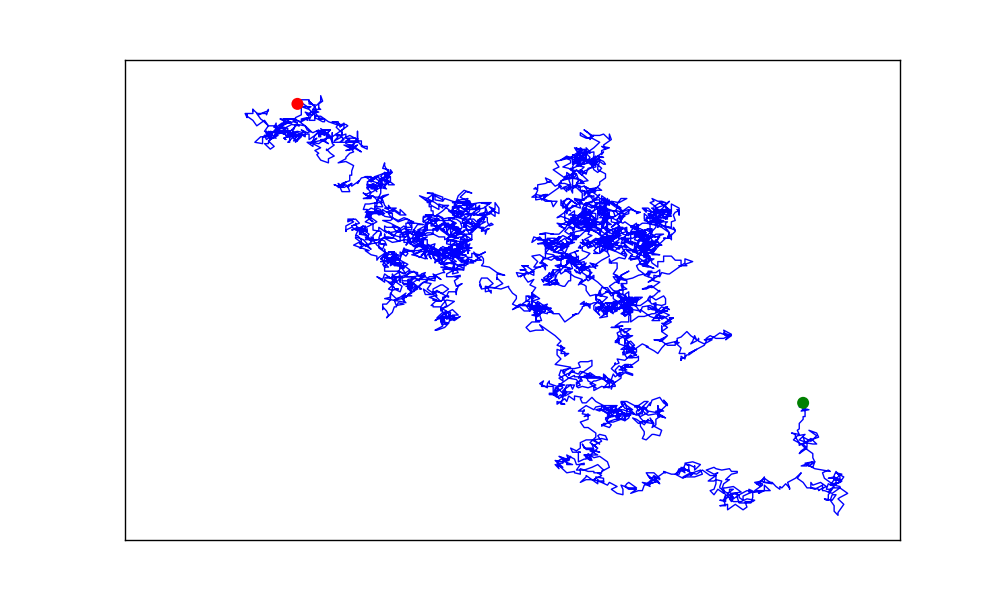
Random walk with 5000 points, connected by lines, with beginning and end points plotted on top of lines

top

15-5: Refactoring

The method fill_walk() is lengthy. Create a new method called get_step() to determine the direction and distance for each step, and then calculate the step. You should end up with two calls to get_step() in fill_walk():

x_step = get_step()
y_step = get_step()

This refactoring should reduce the size of fill_walk() and make the method easier to read and understand.

random_walk.py:

from random import choice

class RandomWalk():
    """A class to generate random walks."""
    
    def __init__(self, num_points=5000):
        """Initialize attributes of a walk."""
        self.num_points = num_points
        
        # All walks start at (0, 0).
        self.x_values = [0]
        self.y_values = [0]

    def get_step(self):
        """Determine the direction and distance for a step."""
        direction = choice([1, -1])
        distance = choice([0, 1, 2, 3, 4])
        step = direction * distance
        return step

    def fill_walk(self):
        """Calculate all the points in the walk."""
        
        # Keep taking steps until the walk reaches the desired length.
        while len(self.x_values) < self.num_points:
            
            # Decide which direction to go, and how far to go in that direction.
            x_step = self.get_step()
            y_step = self.get_step()
            
            # Reject moves that go nowhere.
            if x_step == 0 and y_step == 0:
                continue
            
            # Calculate the next x and y values.
            next_x = self.x_values[-1] + x_step
            next_y = self.y_values[-1] + y_step
            
            self.x_values.append(next_x)
            self.y_values.append(next_y)

Output:

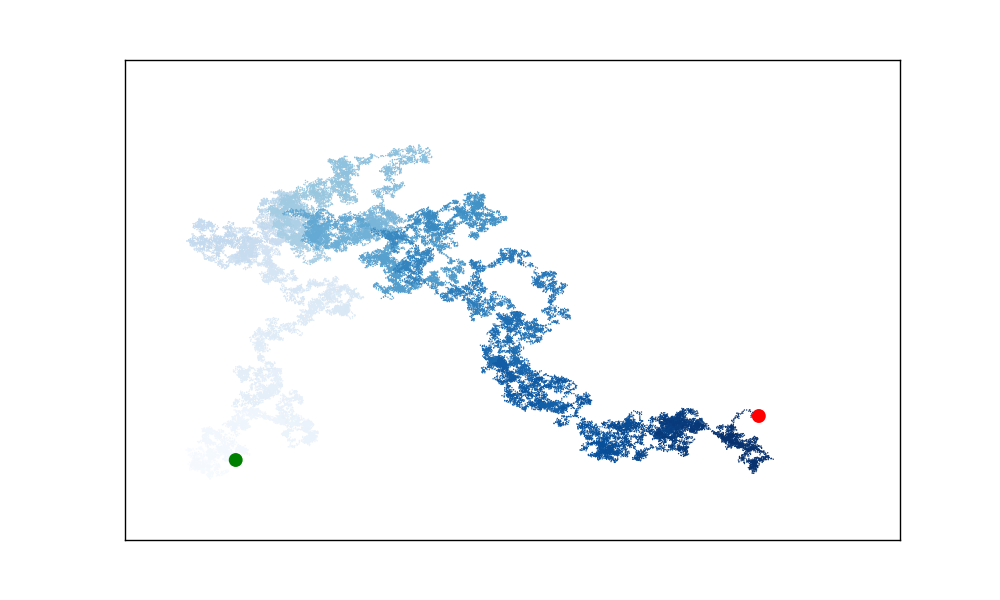
Random walk with 50000 points

top

15-6: Automatic Labels

Modify die.py and dice_visual.py by replacing the list we used to set the value of hist.x_labels with a loop to generate this list automatically. If you’re comfortable with list comprehensions, try replacing the other for loops in die_visual.py and dice_visual.py with comprehensions as well.

Note: This should say to modify die_visual.py, not die.py. This will be corrected in future printings.

die_visual.py:

import pygal

from die import Die

# Create a D6.
die = Die()

# Make some rolls, and store results in a list.
results = [die.roll() for roll_num in range(1000)]
    
# Analyze the results.
frequencies = [results.count(value) for value in range(1, die.num_sides+1)]
    
# Visualize the results.
hist = pygal.Bar()

hist.title = "Results of rolling one D6 1000 times."
hist.x_labels = [str(x) for x in range(1, die.num_sides+1)]
hist.x_title = "Result"
hist.y_title = "Frequency of Result"

hist.add('D6', frequencies)
hist.render_to_file('die_visual.svg')

dice_visual.py:

import pygal

from die import Die

# Create two D6 dice.
die_1 = Die()
die_2 = Die()

# Make some rolls, and store results in a list.
results = [die_1.roll() + die_2.roll() for roll_num in range(1000)]
    
# Analyze the results.
max_result = die_1.num_sides + die_2.num_sides
frequencies = [results.count(value) for value in range(2, max_result+1)]
    
# Visualize the results.
hist = pygal.Bar()

hist.title = "Results of rolling two D6 dice 1000 times."
hist.x_labels = [str(x) for x in range(2, max_result+1)]
hist.x_title = "Result"
hist.y_title = "Frequency of Result"

hist.add('D6 + D6', frequencies)
hist.render_to_file('dice_visual.svg')

top

15-7: Two D8s

Create a simulation showing what happens if you roll two eight-sided dice 1000 times. Increase the number of rolls gradually until you start to see the limits of your system’s capabilities.

import pygal

from die import Die

# Create two D8 dice.
die_1 = Die(8)
die_2 = Die(8)

# Make some rolls, and store results in a list.
results = []
for roll_num in range(1000000):
    result = die_1.roll() + die_2.roll()
    results.append(result)
    
# Analyze the results.
frequencies = []
max_result = die_1.num_sides + die_2.num_sides
for value in range(2, max_result+1):
    frequency = results.count(value)
    frequencies.append(frequency)
    
# Visualize the results.
hist = pygal.Bar()

hist.title = "Results of rolling two D8 dice 1,000,000 times."
hist.x_labels = [str(x) for x in range(2, max_result+1)]
hist.x_title = "Result"
hist.y_title = "Frequency of Result"

hist.add('D8 + D8', frequencies)
hist.render_to_file('dice_visual.svg')

Note: This solution only uses a list comprehension for the hist.x_labels parameter. You might want to try replacing the other loops with comprehensions as well.

Output:

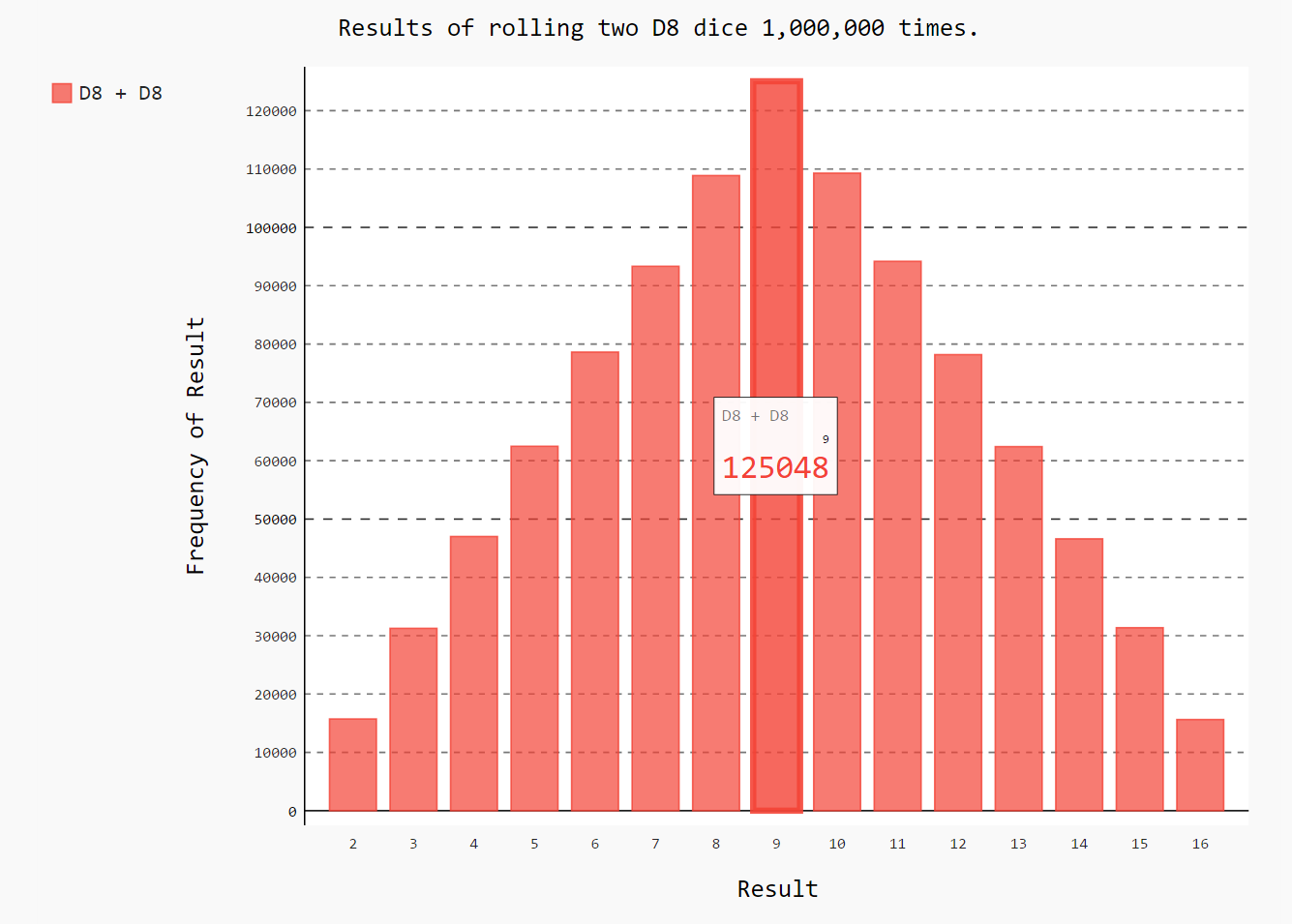
Graph of results of rolling two D8 dice, one million times

top

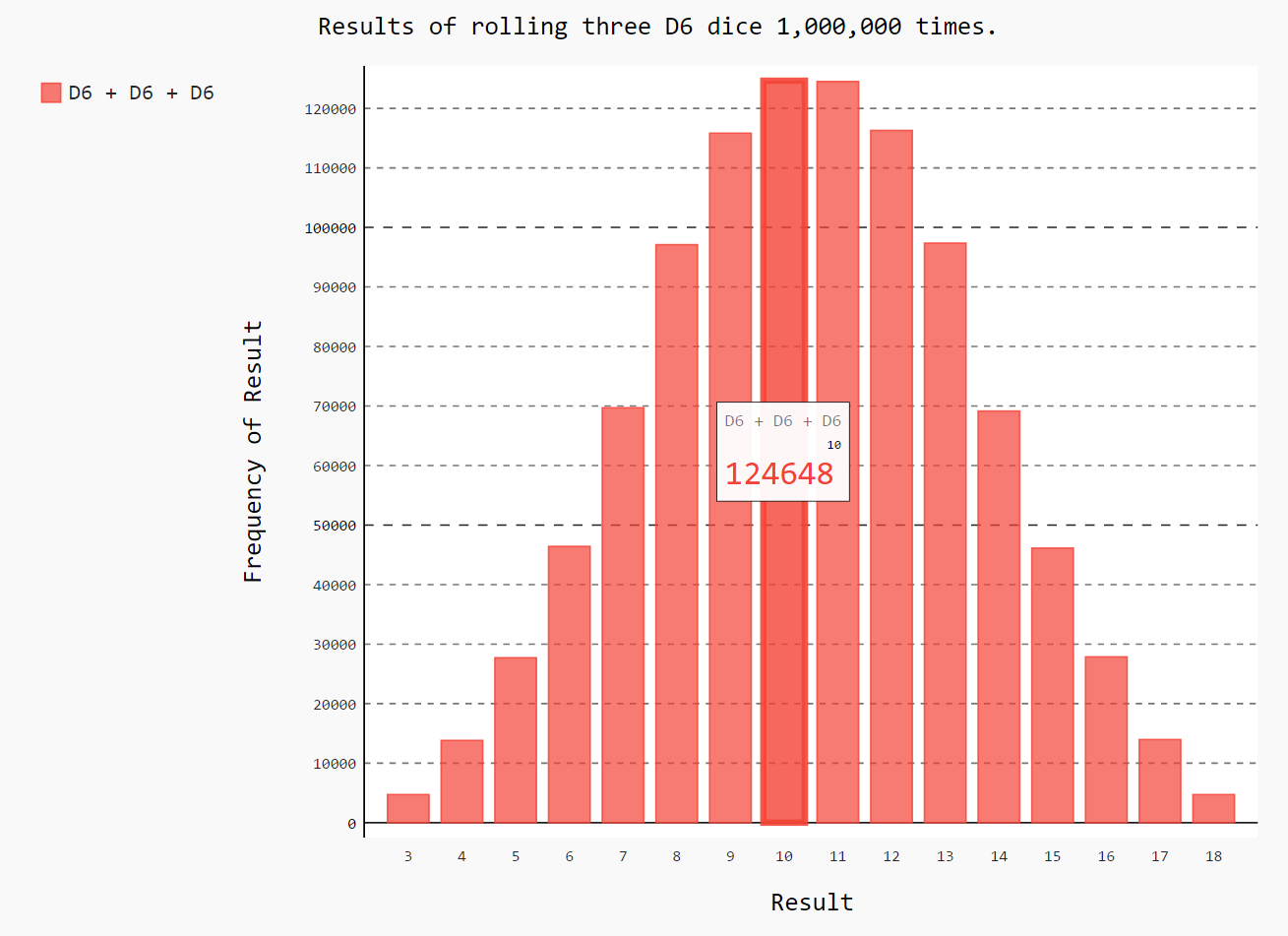
15-8: Three Dice

If you roll three D6 dice, the smallest number you can roll is 3 and the largest number is 18. Create a visualization that shows what happens when you roll three D6 dice.

import pygal

from die import Die

# Create three D6 dice.
die_1 = Die()
die_2 = Die()
die_3 = Die()

# Make some rolls, and store results in a list.
results = []
for roll_num in range(1000000):
    result = die_1.roll() + die_2.roll() + die_3.roll()
    results.append(result)
    
# Analyze the results.
frequencies = []
max_result = die_1.num_sides + die_2.num_sides + die_3.num_sides
for value in range(3, max_result+1):
    frequency = results.count(value)
    frequencies.append(frequency)
    
# Visualize the results.
hist = pygal.Bar()

hist.title = "Results of rolling three D6 dice 1,000,000 times."
hist.x_labels = [str(x) for x in range(3, max_result+1)]
hist.x_title = "Result"
hist.y_title = "Frequency of Result"

hist.add('D6 + D6 + D6', frequencies)
hist.render_to_file('dice_visual.svg')

Note: This solution only uses a list comprehension for the hist.x_labels parameter. You might want to try replacing the other loops with comprehensions as well.

Output:

Graph of results of rolling three D6 dice, one million times

top

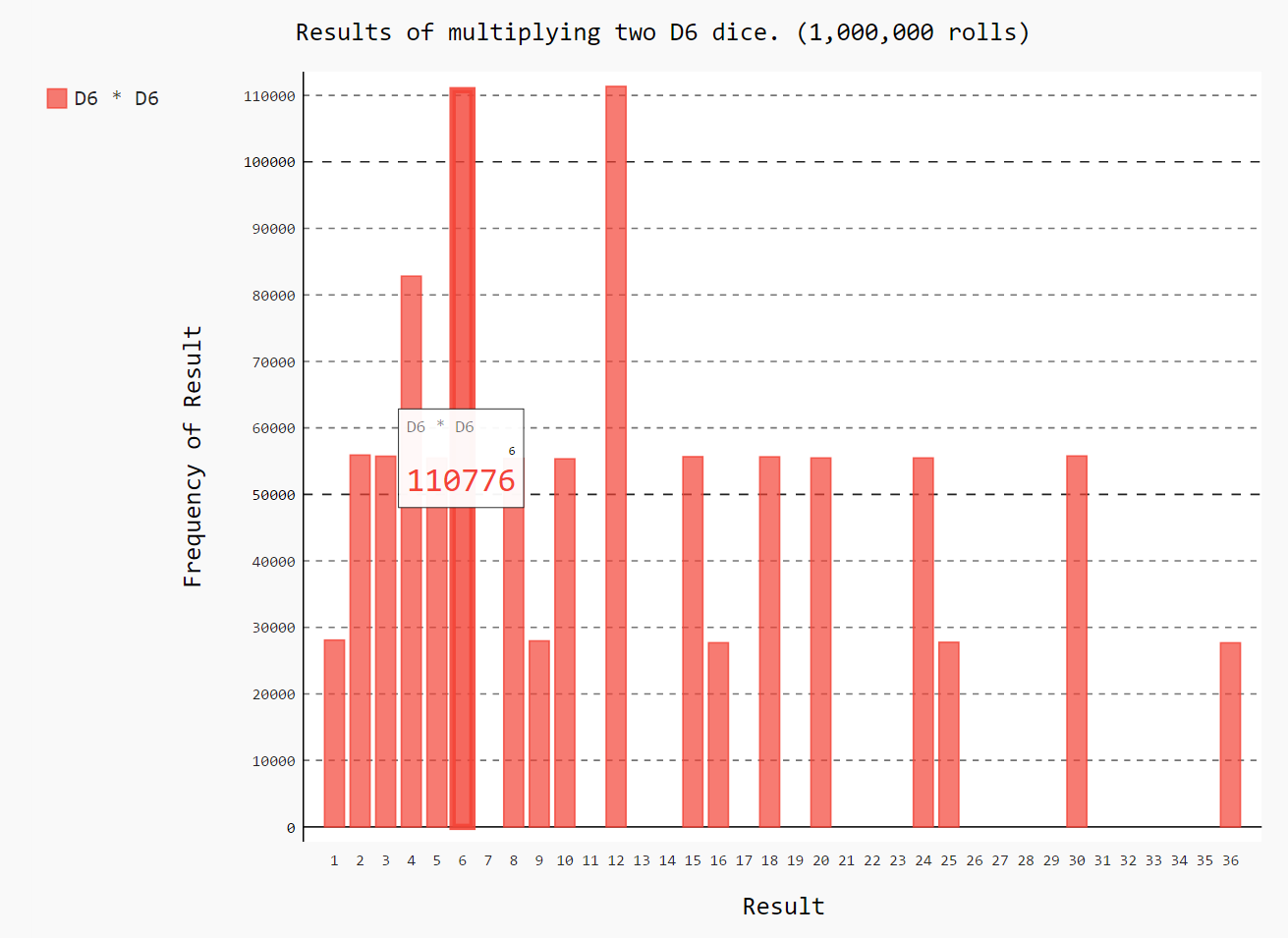
15-9: Multiplication

When you roll two dice, you usually add the two numbers together to get the result. Create a visualization that shows what happens if you multiply these numbers instead.

import pygal

from die import Die

# Create two D6 dice.
die_1 = Die()
die_2 = Die()

# Make some rolls, and store results in a list.
results = []
for roll_num in range(1000000):
    result = die_1.roll() * die_2.roll()
    results.append(result)
    
# Analyze the results.
frequencies = []
max_result = die_1.num_sides * die_2.num_sides
for value in range(1, max_result+1):
    frequency = results.count(value)
    frequencies.append(frequency)
    
# Visualize the results.
hist = pygal.Bar()

hist.title = "Results of multiplying two D6 dice. (1,000,000 rolls)"
hist.x_labels = [str(x) for x in range(1, max_result+1)]
hist.x_title = "Result"
hist.y_title = "Frequency of Result"

hist.add('D6 * D6', frequencies)
hist.render_to_file('dice_visual.svg')

Note: This solution only uses a list comprehension for the hist.x_labels parameter. You might want to try replacing the other loops with comprehensions as well.

Output:

Graph of results of multiplying two D6 dice, one million times

top